Elk jaar vieren wiskundigen op 14 maart Pi-dag met taart (Engels: pie) en pizza. Maar komende zondag is de dag van pi’s concurrent: tau. Tau is de constante 6,28 en daarom valt zijn feestdag op de 28ste van de 6de maand.
Van tau heb je waarschijnlijk nog niet eerder gehoord, maar vast wel al van pi. Het getal pi (3,14….) is de wiskundige constante die de verhouding van de omtrek en de diameter van een cirkel aangeeft. Je herkent hem wellicht van de bijbehorende formule waarmee je de omtrek van een cirkel kunt berekenen: omtrek = pi * diameter, of omtrek = 2 * pi * straal. Pi wordt in veel verschillende formules en toepassingen gebruikt. Maar inmiddels is er een andere wiskundige constante voorgesteld om pi te vervangen: tau.
- Letter Tau
- Letter Pi
De twee wiskundige constanten pi en tau zijn sterk met elkaar verbonden. Tau geeft namelijk de verhouding van de omtrek en de radius van een cirkel aan en is daarom 2 keer pi. Ofwel: tau = 2 x 3,14 = 6,28. De formule voor de omtrek van een cirkel wordt dan: omtrek = tau * straal.
Het idee om pi te vervangen voor een andere constante, is afkomstig van hoogleraar Bob Palais van de Utah Valley University. Hij beschreef dit in zijn opiniestuk Pi is wrong! uit 2001. Palais vindt namelijk dat pi onhandig gedefinieerd is.
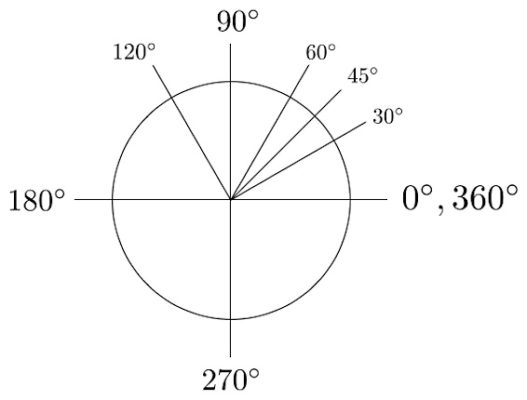
- Figuur 1a: Een aantal belangrijke hoeken van een cirkel, uitgedrukt in booggraden
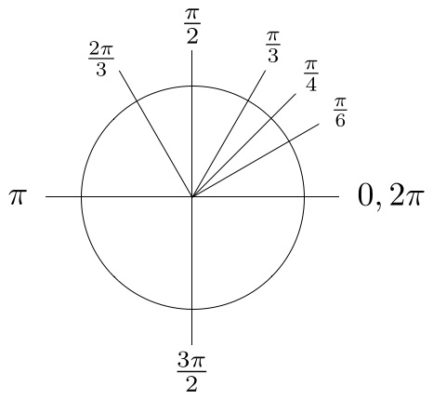
- Figuur 1b: Dezelfde belangrijke hoeken van een cirkel, uitgedrukt in pi-radialen
Hoeken van een cirkel
Zijn grootste bezwaar is dat pi een onhandige keuze is geweest om hoeken van cirkels aan te geven. Op school leren kinderen namelijk dat de hoek van een hele cirkel 360 graden is (Figuur 1a) en dat deze graden ook kunnen worden uitgedrukt in radialen. Dan is de hoek van een hele cirkel 2 pi. Verder is een kwart van een cirkel een half pi, een halve cirkel 1 pi en driekwart cirkel anderhalf pi (Figuur 1b).
Bij het lezen van dit stuk merkte je het misschien al: deze indeling voelt wat onlogisch. Want door de hele cirkel met 2 pi aan te duiden kom je op de onlogische waarden uit dat een kwart van de cirkel een half pi is, terwijl de halve cirkel een heel pi is. Dat rekent nogal onhandig. Het zou veel makkelijker zijn als één omwenteling van een cirkel wordt aangeduid met één symbool.
Definitie van tau
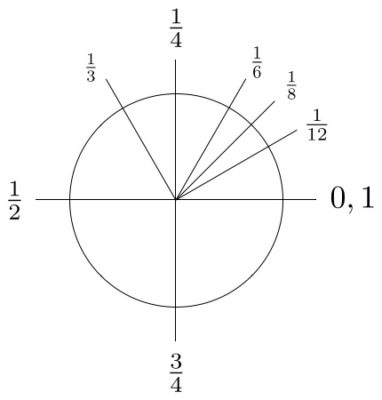
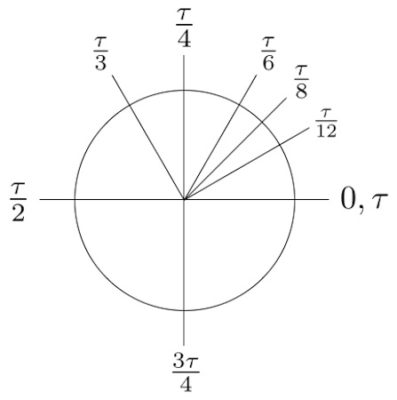
Dit is precies hoe tau is gedefinieerd, namelijk als tau = 2 pi. Dan is de hoek van de hele cirkel 1 tau radialen in plaats van 2 pi radialen. En dan volgt dat een kwart cirkel een kwart tau is, een halve cirkel een half tau en driekwart cirkel is driekwart tau (Figuur 2a en 2b). Zie je die mooie regelmaat? Dit is een stuk natuurlijker en logischer dan dezelfde hoeken uitgedrukt in pi, toch?
- Figuur 2a: Dezelfde belangrijke hoeken van een cirkel, uitgedrukt in breuken
- Figuur 2b: Dezelfde belangrijke hoeken van een cirkel, uitgedrukt in tau radialen
Sinus en cosinus
Ook de twee cirkelfuncties sinus en cosinus worden wat inzichtelijker als we tau gebruiken voor één omwenteling van de cirkel. Sinus en cosinus zijn de twee functies die de coördinaten (waarden op de horizontale en verticale as) aangeven van punten op de eenheidscirkel. Deze functies herhalen zichzelf bij elke omwenteling om deze cirkel. Daarom worden ze periodieke functies genoemd met een periode van één omwenteling.
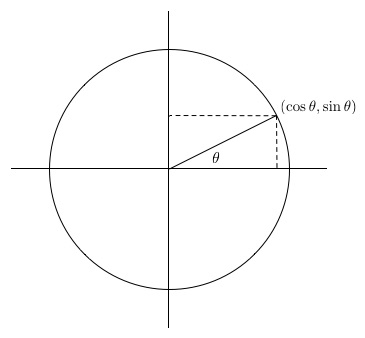
Figuur 3: Sinus en cosinus geven de coördinaten van punten op de eenheidscirkel
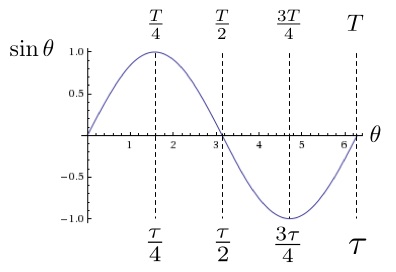
Laten we de sinus als voorbeeld nemen. Deze functie geeft de waarde op de verticale as aan en, zoals ook aangegeven in Figuur 4a, begint bij 0. Wanneer de hoek groter wordt, stijgt de waarde eerst. De functie bereikt zijn maximum 1 bij de bovenkant van de cirkel. Dit is op een kwart van de omwenteling, ofwel een kwart periode. Daarna daalt hij en gaat door het nulpunt bij een halve omwenteling. Vervolgens bereikt hij zijn minimum van -1 bij de onderkant van de cirkel (driekwart) en gaat dan weer terug naar het beginpunt 0 nadat de hele cirkel doorlopen is. In Figuur 4a zijn deze punten weergegeven als functie van radialen, periode T en tau.
- Figuur 4a: Belangrijke punten voor de functie sinus, uitgedrukt in periode T en tau-radialen
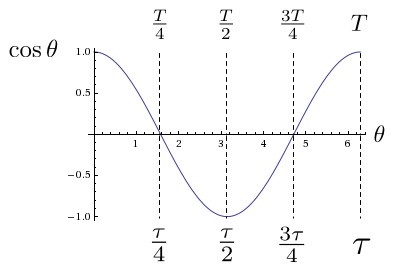
- Figuur 4b: Belangrijke punten voor de functie cosinus, uitgedrukt in periode T en tau-radialen
Mooie regelmaat
Omdat een periode gelijk is aan een omwenteling, is een periode precies 1 tau radialen in plaats van 2 pi radialen. Dus op een kwart van de periode is de hoek een kwart tau radialen, et cetera. We zien hier opnieuw die mooie regelmaat.
Er zijn nog veel meer functies en formules die logischer, mooier of handiger worden als je 2 pi vervangt door 1 tau. Dr. Michael Hartl, een groot voorstander van tau, geeft een aantal voorbeelden in een presentatie over zijn Tau Manifest.
Concurrentiestrijd
Op zich is het idee om pi te vervangen door tau helemaal niet zo gek, omdat dit vele formules inzichtelijker kan maken. Maar er zijn ook argumenten voor het gebruik van pi. Zo heeft ook pi zijn eigen manifest.
Tau’s grootste probleem is waarschijnlijk dat zijn concurrent pi al ruim 250 jaar dé standaard is. Pi wordt momenteel overal gebruikt, dus bij een invoering van tau moeten alle wis- en natuurkundeboeken en ook het lesmateriaal voor scholen worden aangepast. En vergeet de rekenmachines niet: die krijgen een tau-knopje in plaats van een pi-knopje. Online is het makkelijker. Bij Google kun je zowel met pi als met tau rekenen.
Inzichtelijker
De vervanging van pi door tau is een helse klus waar weinigen op zitten te wachten. Bovendien gebruiken vooral wis- en natuurkundigen de meeste formules die handiger worden met de nieuwe constante. Zij zitten echter zó in de materie dat het voor hun begrip van de formules niet zo veel uitmaakt of zij een omwenteling aanduiden met 2 pi of 1 tau.
Maar voor kinderen die leren rekenen met cirkels, kan tau de materie wellicht veel inzichtelijker maken. Misschien zorgt de logica van tau ervoor dat ze dit onderwerp sneller snappen. Daarom is het al een mooie eerste stap als we leerlingen überhaupt vertellen over tau. Dan hoeven we ook niet meteen alle boeken te vervangen, maar kunnen kinderen wel gebruik maken van de mooie regelmaat die tau biedt.
Taugé(taart)?
Zelf heb ik trouwens nog wel een belangrijk argument om pi te behouden. Op Pi-dag hebben we namelijk een goed excuus om taart of pizza te eten. Maar wat voor lekkers past er bij tau? Taugétaart? Zolang Tau-dag geen eigen snack heeft, stel ik voor om pi en tau naast elkaar te gebruiken, zodat we op Pi-dag in ieder geval gewoon taart kunnen blijven eten. Of nog beter: laten we Tau-dag vieren met twee taarten of twee pizza’s. Zo kunnen we nog meer snacken.
Fotocredits:
Hoofdfoto: Talha Khalil via Pixabay
Figuur 1a: Een aantal belangrijke hoeken van een cirkel, uitgedrukt in booggraden
Figuur 1b: Dezelfde belangrijke hoeken van een cirkel, uitgedrukt in pi radialen
Figuur 2a: Dezelfde belangrijke hoeken van een cirkel, uitgedrukt in breuken
Figuur 2b: Dezelfde belangrijke hoeken van een cirkel, uitgedrukt in tau radialen
Figuur 3: Sinus en cosinus geven de coördinaten van punten op de eenheidscirkel.
Figuur 4a: Belangrijke punten voor de functie sinus, uitgedrukt in periode T en tau radialen
Figuur 4b: Belangrijke punten voor de functie cosinus, uitgedrukt in periode T en tau radialen
Bron alle figuren (c) The Tau Manifesto door Dr. Michael Hartl (Met toestemming gebruikt)