De verkiezingen zijn achter de rug en de 150 volksvertegenwoordigers hebben een fysieke zetel in de plenaire zaal van de Tweede Kamer toegewezen gekregen, de zogenoemde zetelindeling. Leeuw of lam lijkt nu de centrale vraag. Heeft de zetelindeling invloed op de rol van de Tweede Kamer in ons bestel? Bepaalt die mede het stemgedrag van de parlementariёrs? Jasper van Doornmalen, Christopher Hojny en Frits Spieksma (TU Eindhoven) gaan dieper in op deze vragen en sluiten af met een revolutionair nieuwe zetelindeling.
Op het eerste gezicht lijkt een zetelindeling misschien niet zo heel belangrijk. Over de meeste kwesties stemmen partijen als een blok. Daarom lijkt de plek waar het kamerlid zit, geen invloed te hebben op het stemgedrag. Toch is dat slechts schijn.
Stemmen zoals de buren
Neem als voorbeeld het parlement van IJsland. Daar worden de 63 gekozen volksvertegenwoordigers willekeurig toegewezen aan de 63 zetels in het IJslandse parlement. Het gevolg hiervan is dat leden van verschillende partijen vaak naast elkaar zitten.
Deze situatie heeft het mogelijk gemaakt om te onderzoeken of stemgedrag van een parlementslid wordt beïnvloed door het stemgedrag van zijn/haar fysieke buren. Een onderzoek uitgevoerd door Saia (2018) heeft laten zien dat dit inderdaad zo is. Met andere woorden: een parlementslid gaat stemmen zoals zijn/haar buren stemmen, en de buren stemmen zoals het parlementslid gaat stemmen. Dat betekent dat de zetelindeling belangrijker is dan in eerste instantie lijkt. De eerste conclusie is dan ook dat de zetelindeling van invloed is op de besluiten die het parlement neemt.
De 150 zetels in de plenaire zaal van de Tweede Kamer zijn verdeeld in zes blokken van 25 zetels. Elk blok bestaat weer uit zes rijen van respectievelijk 2, 3, 4, 5, 5 en 6 zetels. Dit voldoet aan een aantal basisprincipes: de partijen zitten gegroepeerd, de zes grootste partijen bezetten elk twee van de voorste zetels, en er is een traditioneel economische links-rechts afspiegeling van de partijen zichtbaar.
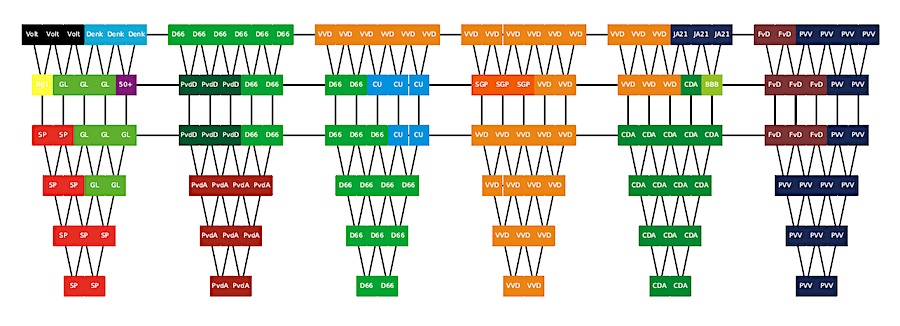
Figuur 1: De huidige zetelindeling in de Tweede Kamer na de verkiezingen van 2021
Alternatieve zetelindeling
Een alternatieve zetelindeling is te vinden door het opstellen en oplossen van een wiskundig model. Zo’n wiskundig model neemt bovengenoemde eisen voor de zetelindeling mee. Het heeft als doelstelling om zoveel mogelijk stoeltjes die bij elkaar in de buurt staan, toe te wijzen aan parlementariërs van dezelfde partij. Het is zaak om dan precies aan te geven welke stoelen bij elkaar in de buurt staan, en welke niet.
In Figuur 2 hieronder staat een schematische schets waarbij zetels die bij elkaar in de buurt liggen, zijn verbonden met een lijn. Vervolgens hebben we zo’n wiskundig model opgesteld en opgelost. De gevonden oplossing staat hier afgebeeld. Deze voldoet aan het links-rechts spectrum van de partijen, en kent de voorste rijen toe aan de zes grootste partijen. In dit geval van links naar rechts SP, PvdA, D66, CDA, VVD en PVV. Verder is deze oplossing optimaal gegroepeerd: zoveel mogelijk zijn de verbonden zetels aan dezelfde partij toegewezen.
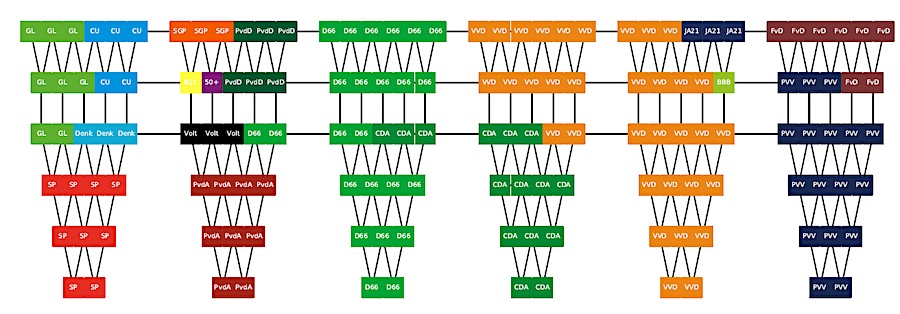
Figuur 2: Optimale zetelindeling
Overeenkomsten en verschillen
Het is aardig om te zien dat, wanneer we beide oplossingen vergelijken, de vertegenwoordigers van JA21 en BBB op precies dezelfde zetels zitten. De verschillen zitten vooral in de positie van Volt en die van het CDA en de VVD. In de optimale oplossing is de VVD over slechts twee blokken verspreid, daar waar de huidige oplossing drie blokken nodig heeft. En hoewel in de huidige situatie alle CDA-zetels in blok 5 zitten, staat op de vijfde rij een CDA-zetel geheel alleen, ingeklemd tussen de BBB en de VVD.
Verder zit Volt in de huidige Kamer geheel links, waar de optimale oplossing Volt in het tweede blok zet. Welke oplossing je ook kiest, er valt altijd wat te mopperen. Maar het is wel zo dat groepering van fracties uitnodigt tot fractiediscipline. Zijn kamerleden dan meer lam dan leeuw? Het voordeel van modelmatige suggesties voor zetelindelingen is dat die objectief en transparant tot stand komen. Dat lijkt geen verkeerde werkwijze in deze politiek rumoerige tijden.
Werkt een andere zetelindeling depolariserend?
In een interview met het AD zei het nieuw gekozen kamerlid Caroline van der Plas (BBB) dat de zetelindeling wilder zou moeten om samenwerking te bevorderen. En inderdaad: het loslaten van het links-rechts spectrum kan een zetelindeling opleveren waarbij parlementsleden van heel verschillende partijen naast elkaar zitten. Lilian Marijnissen zou bijvoorbeeld naast Thierry Baudet kunnen komen te zitten, Simons naast Wilders, en Eerdmans naast Klaver. En aangezien we nu beseffen dat de buren van invloed zijn op het stemgedrag, zal er een depolariserende werking van zo’n zetelindeling uitgaan.
Natuurlijk is het een illusie om te denken dat een ‘wilde’ zetelindeling meningsverschillen laat verdwijnen, maar het is niet vreemd te veronderstellen dat die leidt tot meer samenwerking en meer vertrouwen tussen partijen.
De IJslandse optie
Dus hebben we de IJslandse optie toegepast op de huidige Tweede Kamer: een willekeurige toewijzing van zetels aan partijen. Het is verleidelijk om te speculeren over de consequenties van deze wilde zetelindeling: een homogene opstelling van de Kamerleden ten opzichte van de regering? Wij denken dat dit model de leeuw in de Tweede Kamer een nieuwe kans geeft.
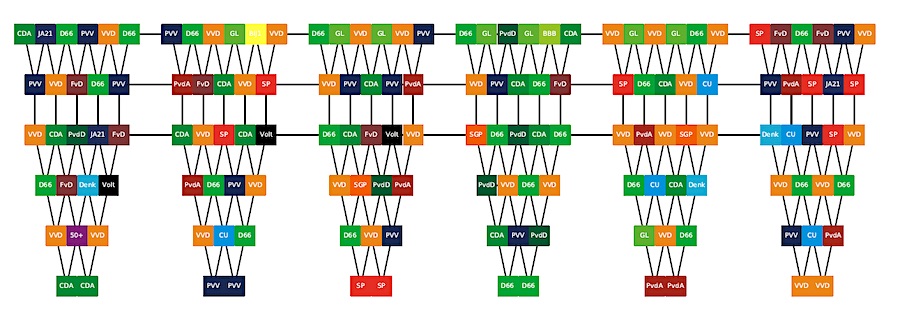
Figuur 3: De IJslandse optie, een wilde zetelindeling in de Tweede Kamer
Overigens, de problematiek van een goede zetelindeling speelt niet alleen in de Tweede Kamer. In gemeenten, provincies en andere nationale parlementen speelt telkens de vraag wie waar komt te zitten. Analytische modellen zijn in staat om op transparante wijze tot objectieve neutrale oplossingen te komen, en kunnen onderdeel zijn van de oplossing.
Tekst en beeld: Jasper van Doornmalen, Christopher Hojny, Frits Spieksma
Department of Mathematics and Computer Science, Group Combinatorial Optimization, TU/e.
Fotocredits en beeld:
Hoofdfoto: Husky, via Wikimedia.nl (CC BY 4.0)
Figuur 1-3: Jasper van Doornmalen, Christopher Hojny, Frits Spieksma
Department of Mathematics and Computer Science, Group Combinatorial Optimization, TU/e. Met toestemming gebruikt.







