Muziekgebouw Eindhoven: een theater gevuld met wiskunde

De maatregelen om de opmars van het coronavirus af te remmen, hebben een enorme impact op de culturele sector. Bioscopen, theatershows, live voorstellingen en muziekoptredens zijn veranderd op een manier die we ons een jaar geleden niet konden voorstellen. Het enerzijds uitvoeren van de anderhalvemeterregel en anderzijds commercieel overleven vormt een enorme uitdaging voor deze sector.

Door Danny Blom, Rudi Pendavingh en Frits Spieksma

Inmiddels bestaat er een heel scala van creatieve ideeën om de culturele sector te redden. Zaalexploitanten moeten bijvoorbeeld zo veel mogelijk mensen toelaten, zonder daarbij de anderhalvemeterregel te overtreden. Hoe doe je dat? Wiskunde biedt daarbij uitkomst.

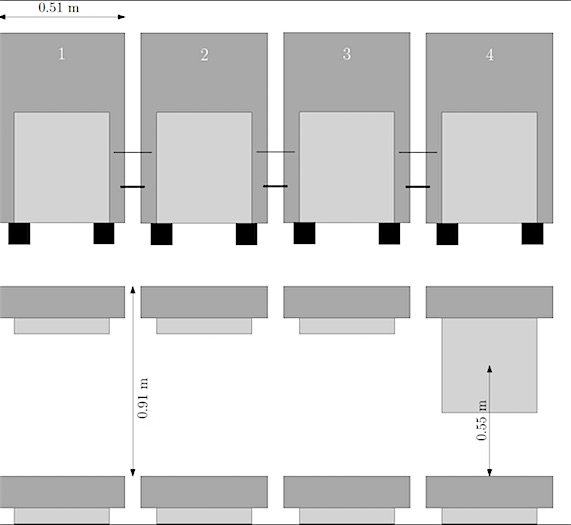
Figuur 1: Voor- en bovenaanzicht van stoelen in het Muziekgebouw Eindhoven, met bijbehorende afmetingen

Wiskundige modellen

Er bestaan wiskundige modellen die deze vraag beantwoorden. De uitkomsten van deze modellen worden gebruikt door het Muziekgebouw Eindhoven (MGE). Kort gezegd komt het erop neer dat het mogelijk is om ongeveer 70 procent van de capaciteit te benutten wanneer een show twee keer op een avond opgevoerd wordt. Hierbij wordt voldaan aan de eis dat bezoekers die niet tot dezelfde familie behoren, minstens anderhalve meter uit elkaar zitten. Bovendien mag elke stoel gedurende een hele avond door ten hoogste één bezoeker gebruikt worden.

We gaan nu wat dieper in op de gebruikte modellen en methoden, waarbij het MGE als voorbeeld dient (zie bovenstaande Figuur 1 voor precieze afmetingen). Het MGE kent twee zalen: de Kleine Zaal met 400 stoelen en de Grote Zaal met 1250 stoelen. Aangezien leden van eenzelfde familie naast elkaar mogen zitten, is het van belang te weten hoeveel families van welke grootte naar de voorstelling komen.

Historische data

Deze informatie is te halen uit historische data van het MGE. Dus van het publiek in het Muziekgebouw is met grote nauwkeurigheid bekend hoeveel families bestaan uit 1 persoon, uit 2 personen, uit 3 personen en uit 4 personen. Deze informatie over familiegroottes noemen we een profiel van reserveringen.

Verder is een relevant meetkundig concept in het model een trapezoïde. Dat is een vierhoek waarvan minstens twee tegenoverliggende zijden evenwijdig zijn (zie onderstaande Figuur 2).

Figuur 2: Door (virtueel) niet-overlappende trapezoïden te plaatsen over de stoelen, kunnen we garanderen dat mensen uit verschillende families ver genoeg uit elkaar zitten. De groene stoelen zijn bezet door twee personen van dezelfde familie. De rode stoelen blijven leeg

Profiel van reserveringen

Het blijkt nu dat een toewijzing van families aan stoelen overeenkomt met het plaatsen van elkaar niet-overlappende trapezoïden. Elke trapezoïde komt overeen met het plaatsen van de leden van een familie van een bepaalde grootte op de stoelen in het ‘centrum’ van de trapezoïde. Op deze manier blijft de anderhalvemetermaatregel gehandhaafd.

Vervolgens is het probleem om zoveel mogelijk, elkaar niet-overlappende trapezoïden, te plaatsen als een zogenaamd geheeltallig programmeringsprobleem gemodelleerd. Bekende methodes dienen om het resulterende model op te lossen.

In dit model is sprake van een doelstellingsfunctie, dat wil zeggen zoveel mogelijk bezoekers toelaten. Bovendien zijn er beperkingen die ervoor zorgen dat de trapezoïden elkaar niet overlappen, zodat de anderhalvemeter wordt gehandhaafd. Daarnaast moet de oplossing overeenkomen met het profiel van reserveringen, en een stoel mag ten hoogste één keer per avond worden gebruikt.

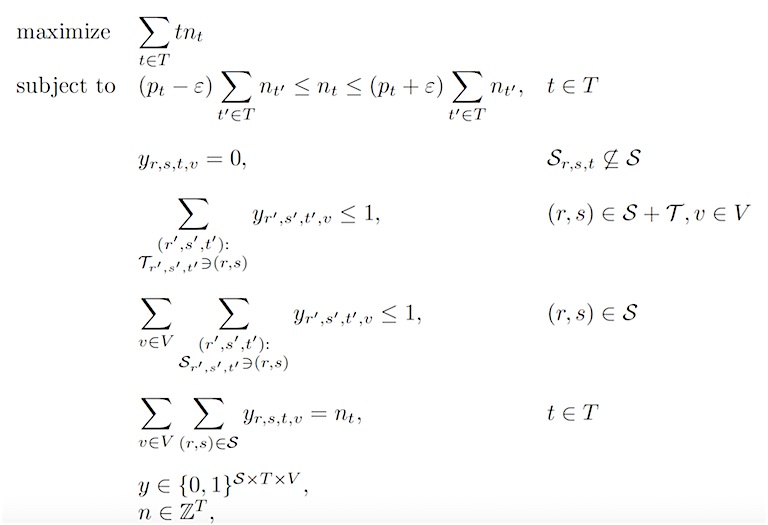
Figuur 3: Het trapezoïde-model geformuleerd als geheeltallig lineair programma

Optimale bezetting

Oplossingen van dit model wijzen uit dat wanneer we ons beperken tot een enkele show op een avond, het onmogelijk is om meer dan eenderde van de capaciteit te benutten bij een realistisch profiel van reserveringen. Maar wanneer er twee opeenvolgende shows op een avond plaatsvinden, is het mogelijk om tot 70 procent van de stoelen te bezetten. Daarbij is voldaan aan de beperking dat een stoel slechts één keer mag worden gebruikt.

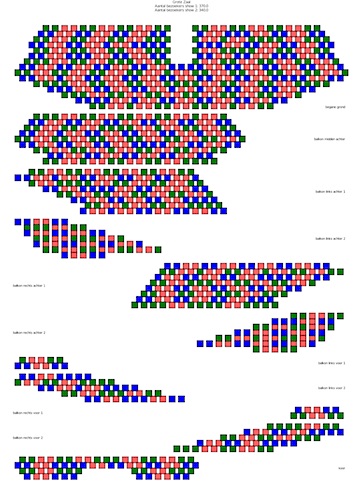
Figuur 4a geeft een illustratie van een optimale benutting van de capaciteit van de Grote Zaal van het MGE, op basis van een profiel van reserveringen uit historische data.

Groen betekent: stoel gebruikt in show 1. Blauw: stoel gebruikt in show 2. Rood: stoel niet gebruikt.

Verschillende theaters gebruiken oplossingen waarbij de rijen ‘om en om’ worden gebruikt. Dat wil zeggen alleen op de even of oneven rijen zijn de stoelen bezet. Vanuit logistiek oogpunt hebben deze oplossingen voordelen. Het is immers makkelijker om mensen naar hun plek te begeleiden. Bovenstaand wiskundige model laat zien dat, ten opzichte van optimale uitkomsten, dit type oplossingen leidt ongeveer 10 procent minder bezetting dan mogelijk (Zie Figuur 4b voor de ‘om en om’-oplossing voor het Muziekgebouw Eindhoven).

Wiskundige technieken maken het dus mogelijk om in de anderhalvemeter-economie de capaciteit van een theater of stadion maximaal te vullen. Het MGE gebruikt deze technieken om oplossingen te vinden die leiden tot een bezettingsgraad van ongeveer 70 procent (met twee voorstellingen per avond). Zogenaamde ‘om en om’-oplossingen zijn logistiek wellicht aantrekkelijk, maar leiden wel tot ongeveer 10 procent minder bezetting.

D. Blom, R. Pendavingh, F.C.R. Spieksma (2020), Filling a theatre in times of corona, Internal Report TU/e.

Fotocredits:
Hoofdfoto: Muziekgebouw Eindhoven (c) Muziekgebouw Eindhoven

Alle illustraties (c) Blom, Pendavingh, Spieksma, TU Eindhoven. Met toestemming gebruikt